Cách tính giá trị lượng giác của một cung hoặc của một góc
Trong bài viết này các bạn sẽ được cung cấp các khái niệm về góc lượng giác, cung lượng giác, hệ thức Sác lơ, và giá trị lượng giác của cung (góc), …
Các kiến thức và kỹ năng này sẽ là nền tảng quan trọng giúp bạn thuận tiện tiếp cận hơn với các khái niệm về các hàm số lượng giác. Vận nên các bạn quan tâm nhé !
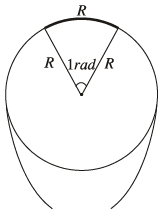
#1. Đơn vị rađian và độ
Các Phần Chính Bài Viết
USD 1 ^ r = \ left ( \ frac { 180 } { \ pi } \ right ) ^ o USD
USD 1 ^ o = \ left ( \ frac { \ pi } { 180 } \ right ) ^ r USD
Công thức liên hệ giữa số đo $ \ alpha USD rađian của góc USD a $ độ là $ \ alpha = \ frac { a \ pi } { 180 } $
Bảng quy đổi 1 số ít góc đặc biệt quan trọng thường gặp trong quy trình học tập, kiểm tra và thi tuyển .
Độ $30^o$ $45^o$ $60^o$ $90^o$ $120^o$ $135^o$ $150^o$ $180^o$ Rađian $\frac{\pi}{6}$ $\frac{\pi}{4}$ $\frac{\pi}{3}$ $\frac{\pi}{2}$ $\frac{2\pi}{3}$ $\frac{3\pi}{4}$ $\frac{5\pi}{6}$ $\pi$
#2. Góc lượng giác
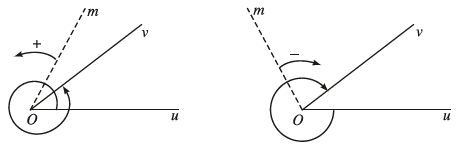
Cho tia $ Om $ quay quanh gốc O
Nếu tia $ Om $ xuất phát từ vị trí của tia $ Ou $ và dừng lại ở vị trí của tia $ Ov $
Lúc này, tất cả chúng ta nói $ Om $ đã quay một góc lượng giác có tia đầu $ Ou $ và tia cuối $ Ov $ và thường được ký hiệu là USD ( Ou, Ov ) USD
Có vô số góc lượng giác có tia đầu $ Ou $ và tia cuối $ Ov $
Nếu có một góc USD ( Ou, Ov ) USD có số đo USD a ^ o USD hoặc $ \ alpha ^ r USD thì mọi góc lượng giác tia đầu $ Ou $ và tia cuối $ Ov $ có số đo dạng USD a ^ o + k360 USD hoặc $ \ alpha ^ r + k2 \ pi USD với USD k USD là một số nguyên bất kể .
#3. Cung lượng giác
Cho một đường tròn định hướng tâm $ O $
Khi các tia $Ou, Ov$ của góc lượng giác $(Ou, Ov)$ cắt đường tròn định hướng tại các điểm tương ứng $U, V$ thì chúng ta có cung lượng giác
Lúc này điểm $ U $ được gọi là điểm đầu và điểm $ V $ được gọi là điểm cuối .
#4. Hệ thức Sác lơ
Với ba tia $ Ou, Ov, Ow $ tùy ý tất cả chúng ta luôn có công thức sđ USD ( Ou, Ov ) + USD sđ USD ( Ov, Ow ) = $ sđ USD ( Ou, Ow ) + k2 \ pi USD với USD k USD là một số nguyên bất kể .
#5. Giá trị lượng giác của cung (góc)
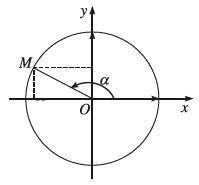
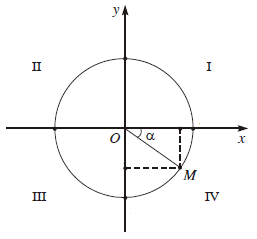
Trên đường tròn lượng giác với hệ trục tọa độ trực chuẩn $Oxy$ cho cung lượng giác
có số đo $\alpha$ và tọa độ điểm $M$ là $(x, y)$
Lúc này tất cả chúng ta có …
- $\sin \alpha=y$
- $\cos \alpha=x$
- Nếu $x$ khác $0$ thì $\tan \alpha=\frac{y}{x}$
- Nếu $y$ khác $0$ thì $\cot \alpha=\frac{x}{y}$
Chú ý:
- $\tan \alpha$ xác định với mọi $\alpha \neq \frac{\pi}{2}+k\pi$ với $k$ là một số nguyên bất kỳ.
- $\cot \alpha$ xác định với mọi $\alpha \neq k\pi$ với $k$ là một số nguyên bất kỳ.
5.1. Dấu của các giá trị lượng giác của cung
Dấu của các giá trị lượng giác của cung $ \ alpha USD nhờ vào vào vị trí điểm cuối USD M $ của cung lượng giác có số đo $ \ alpha USD trên đường tròn lượng giác .
$M$ thuộc góc phần tư Giá trị lượng giác của $\alpha$
I II III IV $\cos \alpha$ $+$ $-$ $-$ $+$ $\sin \alpha$ $+$ $+$ $-$ $-$ $\tan \alpha$ $+$ $-$ $+$ $-$ $\cot \alpha$ $+$ $-$ $+$ $-$ 5.2. Giá trị lượng giác của các cung (góc) lượng giác đặc biệt
Máy tính cầm tay CASIO fx 580 việt nam X hoàn toàn có thể tính được giá trị lượng giác $ \ sin USD, $ \ cos USD, $ \ tan USD và $ \ cot USD của một cung ( góc ) bất kể .Tuy nhiên với những cung ( góc ) đặc biệt quan trọng tất cả chúng ta vẫn nên ghi nhớ chúng :
$\alpha$ $0$ $\frac{\pi}{6}$ $\frac{\pi}{4}$ $\frac{\pi}{3}$ $\frac{\pi}{2}$ $\sin \alpha$ $0$ $\frac{1}{2}$ $\frac{\sqrt{2}}{2}$ $\frac{\sqrt{3}}{2}$ $1$ $\cos \alpha$ $1$ $\frac{\sqrt{3}}{2}$ $\frac{\sqrt{2}}{2}$ $\frac{1}{2}$ $0$ $\tan \alpha$ $0$ $\frac{1}{\sqrt{3}}$ $1$ $\sqrt{3}$ $||$ $\cot \alpha$ $||$ $\sqrt{3}$ $1$ $\frac{1}{\sqrt{3}}$ $0$
#6. Các công thức lượng giác cơ bản
Dưới đây là các công thức lượng giác cơ bản nhất, chúng còn được gọi là các hằng đẳng thức lượng giác đáng nhớ:
- USD \ sin ^ 2 \ alpha + \ cos ^ 2 \ alpha = 1 USD
- USD \ tan \ alpha \ cot \ alpha = 1 $ với mọi $ \ alpha USD khác $ \ frac { k \ pi } { 2 } $, USD k USD là một số nguyên bất kể
- USD 1 + \ tan ^ 2 \ alpha = \ frac { 1 } { \ cos ^ 2 \ alpha } $ với mọi $ \ alpha USD khác $ \ frac { \ pi } { 2 } + k \ pi USD, USD k USD là một số nguyên bất kể
- USD 1 + \ cot ^ 2 \ alpha = \ frac { 1 } { \ sin ^ 2 \ alpha } $ với mọi $ \ alpha USD khác USD k \ pi USD, USD k USD là một số nguyên bất kể
- $ \ sin ( \ alpha + k2 \ pi ) = \ sin \ alpha USD với USD k USD là một số nguyên bất kể
- $ \ cos ( \ alpha + k2 \ pi ) = \ cos \ alpha USD với USD k USD là một số nguyên bất kể
- USD – 1 \ leq \ sin \ alpha \ leq 1 USD
- USD – 1 \ leq \ cos \ alpha \ leq 1 USD
#7. Giá trị lượng của các cung (góc) lượng giác có liên quan đặc biệt
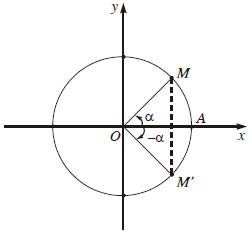
7.1. Hai góc đối nhau
Các điểm cuối của hai cung $\alpha=$ và $-\alpha=$
đối xứng nhau qua trục hoành nên chúng ta có:
$ \ sin ( – \ alpha ) = – \ sin \ alpha USD
$\cos (-\alpha)=\cos \alpha$
USD \ tan ( – \ alpha ) = – \ tan \ alpha USD
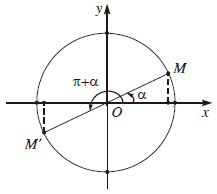
$ \ cot ( – \ alpha ) = – \ cot \ alpha USD7.2. Hai góc hơn kém nhau
Các điểm cuối của hai cung $ \ alpha USD và USD ( \ alpha + \ pi ) USD đối xứng nhau qua gốc tọa độ $ O $ nên tất cả chúng ta có :
$ \ sin ( \ alpha + \ pi ) = – \ sin \ alpha USD
$ \ cos ( \ alpha + \ pi ) = – \ cos \ alpha USD
USD \ tan ( \ alpha + \ pi ) = \ tan \ alpha USD
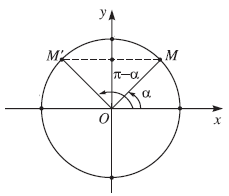
$ \ cot ( \ alpha + \ pi ) = \ cot \ alpha USD7.3. Hai góc bù nhau
Các điểm cuối của hai cung $ \ alpha = $ và $ \ pi – \ alpha = $ đối xứng nhau qua trục tung nên tất cả chúng ta ta có :
$ \ sin ( \ pi – \ alpha ) = \ sin \ alpha USD
$ \ cos ( \ pi – \ alpha ) = – \ cos \ alpha USD
USD \ tan ( \ pi – \ alpha ) = – \ tan \ alpha USD
$ \ cot ( \ pi – \ alpha ) = – \ cot \ alpha USD7.4. Hai góc phụ nhau
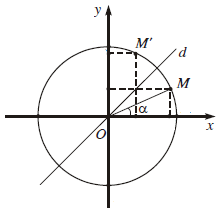
Các điểm cuối của hai cung $ \ alpha USD và $ \ left ( \ frac { \ pi } { 2 } – \ alpha \ right ) USD đối xứng nhau qua đường phân giác USD d USD của góc USD xOy USD nên tất cả chúng ta có :
$ \ sin ( \ frac { \ pi } { 2 } – \ alpha ) = \ cos \ alpha USD
$ \ cos ( \ frac { \ pi } { 2 } – \ alpha ) = \ sin \ alpha USD
USD \ tan ( \ frac { \ pi } { 2 } – \ alpha ) = \ cot \ alpha USD
$ \ cot ( \ frac { \ pi } { 2 } – \ alpha ) = \ tan \ alpha USD
#8. Lời kết
Vâng, như vậy là qua bài viết này thì bạn đã hiểu được khái niệm về góc lượng giác, cung lượng giác, hệ thức Sác lơ, và giá trị lượng giác của cung ( góc ) .. rồi đúng không ?
Thay cho lời kết thì mình sẽ trình làng đến các bạn một thủ pháp máy tính cầm tay giúp quy đổi nhanh số đo góc từ rađian sang độ và ngược lại .Bước 1. Cài đặt đơn vị góc là đơn vị góc mà bạn muốn chuyển đổi:
- Chuyển sang rađian thì cài đặt đơn vị góc là Radian
- Chuyển sang độ thì cài đặt đơn vị góc là Degree
Nhấn lần lượt các phím
cài đặt đơn vị góc là rađian.
Nhấn lần lượt các phím
để cài đặt đơn vị góc là độ.
Bước 2. Nhập số đo góc cần chuyển đổi
Bước 3. Nhấn phím
=> nhấn phím
=> chọn đơn vị cho góc vừa nhập
Bước 4. Nhấn phím
Hi vọng mẹo nhỏ trong bài viết này sẽ có ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
Bài viết đạt : 5/5 sao – ( Có 1 lượt nhìn nhận )
Source: https://suachuatulanh.org
Category : Tư Vấn
Có thể bạn quan tâm
- Lỗi H-29 tủ lạnh Sharp Side by Side dẫn đến hỏng toàn diện (27/11/2024)
- 12 Cách Để Giấy Dán Trần Có Độ Bền Lâu Nhất Luôn Mới (23/11/2024)
- Lỗi E-45 Máy Giặt Electrolux Nguy Hiểm Cho Bo Mạch! (21/11/2024)
- Tủ lạnh Sharp lỗi H-28 Những bước cần làm ngay (16/11/2024)
- Lỗi H27 tủ lạnh Sharp và các bước sửa đơn giản (07/11/2024)
- Giải mã lỗi E-42 máy giặt Electrolux ai cũng hiểu (01/11/2024)
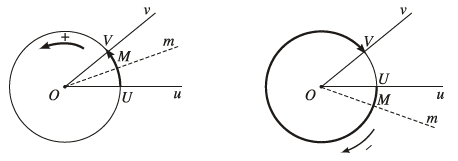
![Bảo Hành Tủ Lạnh Sharp Ủy Quyền Tại Hà Nội [0941 559 995]](https://suachuatulanh.org/wp-content/uploads/bao-hanh-tu-lanh-sharp-2-300x180.jpg)
