Công suất và hiệu suất của nguồn điện | Vật Lý Đại Cương
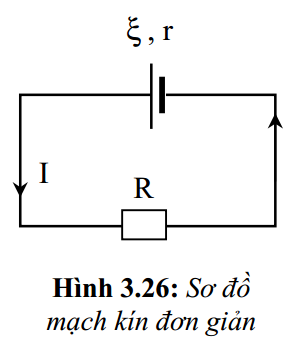
Xét mạch kín như hình 3.26. Trường lực lạ sinh công để “ bơm ” dòng điện chạy trong mạch. Công của nguồn điện chính là công của trường lực lạ và công này chuyển hóa thành công xuất sắc của dòng điện. Do đó, công suất của nguồn điện bằng công suất của dòng điện trong toàn mạch :Pn = Ptoàn mạch = UI + I2r = I2 ( R + r )Mà theo định luật Ohm mạch kín : \ ( I = \ frac { \ xi } { R + r } \ )
Do đó, công suất của nguồn điện là: \( {{P}_{n}}=\xi I \) (3.57)
Bạn đang đọc: Công suất và hiệu suất của nguồn điện | Vật Lý Đại Cương
Vậy, công suất của một nguồn điện bằng tích suất điện động của nguồn với cường độ dòng điện qua nguồn đó .Khi nguồn phát điện, một phần nguồn năng lượng của nguồn cung ứng cho mạch ngoài hoạt động giải trí – nguồn năng lượng này là có ích ; một phần nguồn năng lượng chuyển thành nhiệt làm nóng nguồn ( do nguồn có điện trở nội ) – nguồn năng lượng này là vô ích. Gọi Pn là công suất của nguồn điện, Phi là công suất hữu dụng thì tỉ số : \ ( H = \ frac { { { P } _ { hi } } } { { { P } _ { n } } } \ )Được gọi là hiệu suất của nguồn điện .Ta có : \ ( H = \ frac { { { P } _ { hi } } } { { { P } _ { n } } } = \ frac { { { P } _ { n } } – { { I } ^ { 2 } } r } { { { P } _ { n } } } = \ frac { \ xi I – { { I } ^ { 2 } } r } { \ xi I } = \ frac { \ xi – Ir } { \ xi } = \ frac { R } { R + r } \ ) ( 3.59 )Từ ( 3.59 ) suy ra, hiệu suất của nguồn điện càng cao khi điện trở nội r của nguồn càng nhỏ .Vấn đề đặt ra giờ đây là với một nguồn điện có suất điện động \ ( \ xi \ ) và điện trở trong r cho trước thì nó hoàn toàn có thể cấp ra mạch ngoài một công suất tối đa là bao nhiêu ? Khảo sát yếu tố này, ta thiết lập mạch kín như hình 3.26. Công suất mà nguồn phát ra chính là công suất tiêu thụ của mạch ngoài :
\ ( P = R { { I } ^ { 2 } } = \ frac { { { \ xi } ^ { 2 } } } { { { \ left ( R + r \ right ) } ^ { 2 } } }. R = \ frac { { { \ xi } ^ { 2 } } } { { { \ left ( \ sqrt { R } + \ frac { r } { \ sqrt { R } } \ right ) } ^ { 2 } } } \ ) ( 3.60 )Áp dụng bất đẳng thức Cauchy : \ ( \ sqrt { R } + \ frac { r } { \ sqrt { R } } \ ge 2 \ sqrt { r } \ ), dấu “ = ” khi R = r .Do đó : \ ( P \ le \ frac { { { \ xi } ^ { 2 } } } { 4 r } \ ) ( 3.61 )Vậy, công suất lớn nhất mà nguồn hoàn toàn có thể phát ra mạch ngoài là : \ ( { { P } _ { \ max } } = \ frac { { { \ xi } ^ { 2 } } } { 4 r } \ ) ( 3.62 ) khi điện trở mạch ngoài bằng với điện trở trong của nguồn điện .Công thức ( 3.62 ) được cho phép ta ước tính số nguồn tối thiểu để hoàn toàn có thể cung câp cho một mạch hoạt động giải trí thông thường. Ví dụ, phải dùng tối thiểu bao nhiêu pin loại ( \ ( 6 \ text { } V-1 \ text { } \ Omega \ ) ) để hoàn toàn có thể thắp sáng thông thường bóng đèn ( \ ( 6 \ text { } V-24 \ text { } W \ ) ) ? Để vấn đáp thắc mắc này, thứ nhất ta tính công suất lớn nhất mà mỗi pin hoàn toàn có thể cung ứng là \ ( { { P } _ { \ max } } = \ frac { { { \ xi } ^ { 2 } } } { 4 r } = \ frac { { { 6 } ^ { 2 } } } { 4.1 } = 9 \ text { } W \ ). Mà đèn sáng thông thường thì nó phải tiêu thụ công suất 24 W. Vậy số pin không hề nhỏ hơn 3 .
Xem thêm: Sửa máy điều hòa tại Đồng Nai tốt nhất
Sự biến thiên công suất P. mà nguồn cấp ra mạch ngoài được màn biểu diễn trên đồ thị hình 3.27. Theo đó ta nhận thấy :+ Khi giá trị điện trở R của mạch ngoài tăng từ 0 đến r thì công suất tăng từ 0 đến giá trị cực lớn, rồi giảm dần 0 khi R rất lớn .
+ Luôn có hai giá trị điện trở R1, R2 của mạch ngoài cùng tiêu thực cùng một công suất P < Pmax. Hai giá trị đó chính là nghiệm của phương trình ( 3.60 ). Dễ dàng ta chứng tỏ được : \ ( { { R } _ { 1 } }. { { R } _ { 2 } } = { { r } ^ { 2 } } \ ) ( 3.63 )
Source: https://suachuatulanh.org
Category : Thợ Điều Hòa
Có thể bạn quan tâm
- Cách sửa mã lỗi máy lạnh Carrier cùng chuyên gia App ong Thợ (02/05/2024)
- Cùng xóa các mã lỗi điều hòa Sumikura bởi App Ong Thợ (26/04/2024)
- Cách sửa danh sách mã lỗi máy điều hòa Gree Inverter cùng Ong Thợ (24/04/2024)
- Chỉ 200.000 VNĐ Được Bảo Dưỡng Điều Hòa Chuẩn 9 Bước (22/04/2024)
- Iindex khắc phục máy điều hòa Fujitsu báo lỗi cùng Ong Thợ (21/04/2024)
- Hướng dẫn sửa máy điêu hòa Mitsubishi báo lỗi chuẩn an toàn (19/04/2024)










![Bảo Hành Tủ Lạnh Sharp Ủy Quyền Tại Hà Nội [0941 559 995]](https://suachuatulanh.org/wp-content/uploads/bao-hanh-tu-lanh-sharp-2-300x180.jpg)